Digitization help student to explore and study their academic courses online, as this gives them flexibility and scheduling their learning at their convenience. Kidsfront has prepared unique course material of General Intelligence And Reasoning Direction And Distance for SSC SI CAPF Exam student. This free online General Intelligence And Reasoning study material for SSC SI CAPF Exam will help students in learning and doing practice on Direction And Distance topic of SSC SI CAPF Exam General Intelligence And Reasoning. The study material on Direction And Distance, help SSC SI CAPF Exam General Intelligence And Reasoning students to learn every aspect of Direction And Distance and prepare themselves for exams by doing online test exercise for Direction And Distance, as their study progresses in class. Kidsfront provide unique pattern of learning General Intelligence And Reasoning with free online comprehensive study material and loads of SSC SI CAPF Exam General Intelligence And Reasoning Direction And Distance exercise prepared by the highly professionals team. Students can understand Direction And Distance concept easily and consolidate their learning by doing practice test on Direction And Distance regularly till they excel in General Intelligence And Reasoning Direction And Distance.
 From her home facing south west, Kavita walks 15 m and turns Northward and walks 12 m. How far was she from her home, Which was her starting point?
From her home facing south west, Kavita walks 15 m and turns Northward and walks 12 m. How far was she from her home, Which was her starting point? Correct Answer Is : 9 metres
Correct Answer Is : 9 metres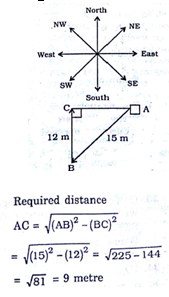
 A man climbing up a wall of 24 metres high. He climbs 16 m on one day but slipped back by 3m 40 cms in the evening. How far had the man reached ?
A man climbing up a wall of 24 metres high. He climbs 16 m on one day but slipped back by 3m 40 cms in the evening. How far had the man reached ? Correct Answer Is : 12.6 m
Correct Answer Is : 12.6 m Keeping her back towards the rising sun, Reshma starts walking. After a few minutes she turns left and keeps on walking. Then a little later she turns right and then left. In
Keeping her back towards the rising sun, Reshma starts walking. After a few minutes she turns left and keeps on walking. Then a little later she turns right and then left. In Correct Answer Is : South or West
Correct Answer Is : South or West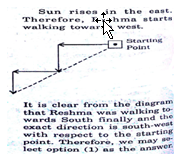
 A person walks towards his house at 8 : 00 am and observed his shadow to his right. In which directions he is walking ?
A person walks towards his house at 8 : 00 am and observed his shadow to his right. In which directions he is walking ? Correct Answer Is : South
Correct Answer Is : South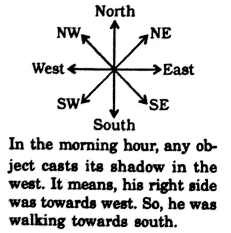
 A boat moves from a jetty towards East. After sailing for 9 nautical miles, She turns towards right and covers another 12 nautical miles. If she wants to go back to the jetty what is the shortest distance now from her present position ?
A boat moves from a jetty towards East. After sailing for 9 nautical miles, She turns towards right and covers another 12 nautical miles. If she wants to go back to the jetty what is the shortest distance now from her present position ? Correct Answer Is : 15 nautical miles
Correct Answer Is : 15 nautical miles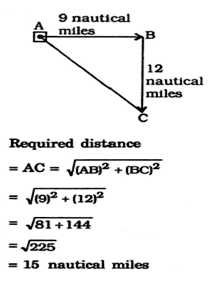
 Six of my colleagues are sitting on the first row in this group photograph. Krishna is to the left of Kumar and to the right of Samy. Vaani is in between Sheela and Kumar.
Six of my colleagues are sitting on the first row in this group photograph. Krishna is to the left of Kumar and to the right of Samy. Vaani is in between Sheela and Kumar.  Correct Answer Is : To the left of Samy
Correct Answer Is : To the left of Samy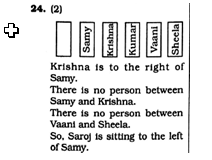
 Rahim rode on his bicycle from his house towards the market for 300 m. He was moving south-west .Then he turned left at an angle of 135° and rode for 100 m to visit a friend. In Which direction is Rahim`s house located from his friend`s house?
Rahim rode on his bicycle from his house towards the market for 300 m. He was moving south-west .Then he turned left at an angle of 135° and rode for 100 m to visit a friend. In Which direction is Rahim`s house located from his friend`s house? Correct Answer Is : North
Correct Answer Is : North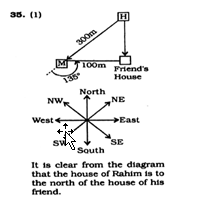
 A postman starts delivering letters 3km southwards and then turns right. He covers 4 km on this road and again turns right. He delivers letters for 3 km and completes his daily beat. Then, he turns left for lunch at home, Which is 5 km away. How far as he to travel to reach the post-office after lunch?
A postman starts delivering letters 3km southwards and then turns right. He covers 4 km on this road and again turns right. He delivers letters for 3 km and completes his daily beat. Then, he turns left for lunch at home, Which is 5 km away. How far as he to travel to reach the post-office after lunch? Correct Answer Is : 9 km
Correct Answer Is : 9 km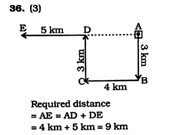
 Arjun start from school and walks 4km towards west, turns right and walks 3km. Then he planned to return back to school, but only in the shortest path. Q.What is the school and the point Q.Where he stopped?
Arjun start from school and walks 4km towards west, turns right and walks 3km. Then he planned to return back to school, but only in the shortest path. Q.What is the school and the point Q.Where he stopped? Correct Answer Is : 5km
Correct Answer Is : 5km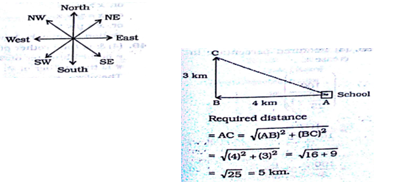
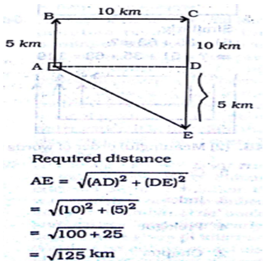
 A man starts journey from home. He goad 5km to the north, then prOceeds 10kms to the right. From there he again turns right and goes 10kms. How far is he from home? All distance are measured aerially.
A man starts journey from home. He goad 5km to the north, then prOceeds 10kms to the right. From there he again turns right and goes 10kms. How far is he from home? All distance are measured aerially. Correct Answer Is : √125
Correct Answer Is : √125